BRYŁY OBROTOWE bst: Zad1. Oblicz objętość i pole ow.bocznej stożka którego promień podstawy r=3 a tworząca nachylona jest do płaszczyzny podstawy pod kątem 60stopni. Zad2. kolo o promieniu 12 podzielono na trzy przystajace wycinki kolowe. Z 1 z nich utworzono pow.boczną stożka. Oblicz wysokosc tego stozka i jego objetosc. zad3. Gałki lodów maja kształt półkoli.Ile razy więcej wazy gałka o promieniu 5cm od gałki o promieniu 4cm.? zad4. Pole powierzchni całkowitej stożka wynosi 301,44dm[kwadratowego] a pole pow.bocznej 188,4dm[kwadratowego] oblicz objetosc tej bryły.

asdf: Zad 1.

	1
V =		πr2 * h
	3

r = 3

	h
tg60o =
	3

	h
√3 =
	3

h = 3√3 Zad 2. http://matma4u.pl/topic/33546-stozek/ Zad 3.

	4
V =		πr3
	3

półkula:

	2
V =		πr3
	3

oblicz jedno i drugie, będziesz mieć odp Zad 4. P_c = 301,44 dm² P_b = 188, 4 dm² P_b = π * r * l P_c = πr(r + l) = π r² + π * r * l Z tego obliczysz r, a później obliczysz tworzącą stożka − dalej z tw. pitagara będziesz mieć wysokość, tutaj już łatwo obliczyć V

bst: asdf co do tego 4 zadania to nie wiem jak to obliczyć... za resztę dzieki wielki. MAM TU JESZCZE KILKA INNYCH ZADAŃ. 1.Dany jest graniastosłup prawidłowy sześciokątny którego wszystkie krawędzie maja jednakowa długość Objętość tego graniastosłupa jest równa 12√3 Wyznacz długość krawędzi tego graniastosłupa. 2. Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy a=8 Krawędź boczna jest nachylona do podstawy pod takim kątem a, że cos a = ²₃ WYznacz V i PB tego ostrosłupa. 3.Suma długości wszystkich krawędzi sześcianu jest rowna 60. Oblicz sumę pol wszystkich ścian tego sześcianu. NAJLEPIEJ ŁOPATOLOGICZNIE KROK PO KROKU CO TRZEBA ROBIĆ. DZIĘKÓWA!

loitzl9006: Co do zad4 ze stożkiem Skoro wiesz, że π*r*l jest równe 188,4 a π*r² + π*r*l = 301,44 , to π*r² = 301,44 − π*r*l czyli π*r² = 301,44 − 188,4 π*r² = 113,04 r=√^113,04_π Teraz, znając już r, z równania π*r*l = 188,4 znajdujesz l, a potem z Pitagorasa r²+H²=l² wyliczasz wysokość H, i potem już możesz policzyć objętość. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Nowe zadania. 1. załóżmy, że ta krawędź graniastosłupa ma długość a zatem długością boku podstawy będzie a, i wysokością graniastosłupa też będzie a. wykorzystujemy fakt, że sześciokąt foremny, jaki jest w podstawie bryły, składa się z sześciu trójkątów równobocznych, każdy o boku długości a. Zatem pole podstawy będzie równe

	a2 √3
Pp = 6*
	4

zaś H=a Wobec tego

	a2 √3		a3 √3
V=Pp * H = 6*		* a = 3*		= 12√3
	4		2

Wyliczamy a.

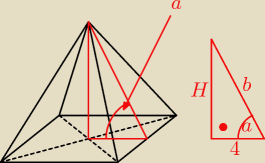
loitzl9006: 2. Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy a=8 Krawędź boczna jest

	2
nachylona do podstawy pod takim kątem a, że cos a =		WYznacz V i PB tego ostrosłupa.
	3

Do obliczenia V potrzebujemy H, zaś do policzenia PB potrzebujemy b. Z podanego cosinusa wiemy,

	4		2
że		=		. Z proporcji wyliczymy b. Później (z Pitagorasa) policzymy H.
	b		3

3.Suma długości wszystkich krawędzi sześcianu jest rowna 60. Oblicz sumę pol wszystkich ścian tego sześcianu. Krawędzi w każdym sześcianie, jak wiadomo, jest 12. Wiadomo też, że krawędzie w sześcianie są tej samej długości (powiedzmy że długość krawędzi sześcianu to a ). Zatem sumę długości wszystkich krawędzi w sześcianie możemy zapisać jako 12a. Znajdujemy a z równania 12a=60 a potem, korzystając z tego, że pole jednej ściany wynosi a², musimy znaleźć ile wynosi 6a² (bo sześcian ma sześć ścian o jednakowym polu każda).

bst: PODZIĘKOWAŁ BÓG CI W DZIECIACH WYNAGRODZI

bst: co do 4 zadania, r wyszło mi 6 l 10 a H 8 V=298,4 wszystko ok? w 2 zad Pb wyszło mi 32√5 H=2√5 a jak obliczyć PP?

bst: 3. a=5 czyli 6a²=150. zajebiście że tak piszesz wszystko bo zaczynam kminić powoli do czwartku się nauczę, mam nadzieję. 1)OKRESL DZIEDZINE WYRAZENIA WYMIERNEGO A ANSTEPNIE WYKONAJ DZIALANIA I PRZEDSTAW WYNIK W JAK NAJPROSTSZEJ POSTACI; (X/X+1+2X−12/x2−1) x 4/x−3 − 3/x−2)= 4) DANA jest funkcja f(x) 12x+5 / 3x+4 a) podaj dziedzine b) oblicz miejsce zerowe c) zapisz rownania asymptot wykresu tej funkcji d) oblicz dla jakiego argumentu funkcja przyjmuje wartosc 1 i 1/4 2) PRZEKSZTAŁĆ WZOR FUNKCJI Z POSTACI OGOLNEJ DO KANONICZNEJ LUB ODWROTNIE A) F(X) = − 4/X−1/3 PLUS CALY UŁĄMEK 7; B) F(X) 1,5X−9 / X+2 3) ROZWIAZ ROWNANIE I NIEROWNOSC A) 4X−16/4−3X = 0 B) X2−5X−3 / X+7 > −1 jeszcze jakbyś mi z tym pomogł to było by super. też tak objaśnione. Z góry dziękuje i pozdrawiam

loitzl9006: mniej−więcej tak, choć V wychodzi mi cały czas ok. 301 ale niech już będzie zad2: Czemu takie Pb? Pb to nic innego jak suma pól czterech trójkątów równoramiennych o długości podstawy a=8 i wysokości b=6

	1
Zatem Pb=4 *		* a * b = 2ab=2*8*6=96
	2

H dobrze obliczyłeś PP to po prostu pole kwadratu o boku 8 zatem PP=8²=64

loitzl9006: co do ułamków to najpierw krótka instrukcja ich zapisywania: https://matematykaszkolna.pl/forum/przyklady9.html potem zapiszesz wszystko jak należy i będziemy rozkminiać

bst: OKRESL DZIEDZINE WYRAZENIA WYMIERNEGO A ANSTEPNIE WYKONAJ DZIALANIA I PRZEDSTAW WYNIK W JAK NAJPROSTSZEJ POSTACI ( ^X_X+1+^2x−12_x²−1 ) * ( ⁴_x−3 − ³_x−2 )=

asdf: wez popraw zapis. Uzywaj duzego "U" przy pisaniu ulamkow

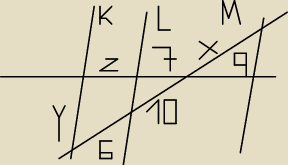
bst: Wiedząc że proste K,L,M są rownoległe oblicz z,y,z POMOCY!

bst: POPRAWIONE.

	X		2X−12		4		3
(		+		) * (		−		) =
	X+1		X2−1		X−3		X−2

2. Przekształć wzór fukcji z postaci ogólnej do kanonicznej lub odwrotnie:

	1
f(x)= − U{4} X −		+ 7 tutaj ma byc − cały ułąmek w liczniku 4 dzielone przez X minus
	3

jedna trzecia i DO CAŁOŚCI PLUS 7 ale nie mogę tego zapisać

	1,5x−9
b) f(x)=
	x+2

ROZWIAŻ ROWNANIE i NIEROWNOSC

	4x−16
a)		= 0
	4−3x

	x2 − 5x − 3
b)		> −1
	x+7

Gustlik: ad 1. Obliczam pierwszy nawias:

x		2x−12		x		2x−12
	+		=		+		=
x+1		x2−1		x+1		(x−1)(x+1)

	x(x−1)+2x−12		x2−x+2x−12		x2−x+2x−12
=		=		=
	(x−1)(x+1)		(x−1)(x+1)		(x−1)(x+1)

	x2+x−12		(x+4)(x−3)
=		=
	(x−1)(x+1)		(x−1)(x+1)

Rozkładam x²+x−12, bo może coś się skrócić z mianownikiem a może później z drugim ułamkiem: Δ=49, √Δ=7, x₁=−4, x₂=3, mamy postać iloczynową trójmianu kwadratowego (x+4)(x−3) Obliczam drugi nawias:

4		3		4(x−2)−3(x−3)
	−		=		=
x−3		x−2		(x−3)(x−2)

	4x−8−3x+9		x+1
=		=
	(x−3)(x−2)		(x−3)(x−2)

Liczę cale wyrażenie i skracam to, co zaznaczyłem takim samym kolorem:

(x+4)(x−3)		x+1
	*		=
(x−1)(x+1)		(x−3)(x−2)

	x+4		1		x+4
=		*		=
	x−1		x−2		(x−1)(x−2)

Założenia − wszystkie mianowniki (przed skróceniem !) ≠ 0: x≠1, x≠−1, x≠3, x≠2 ⇒ D=R\{−1, 1, 2, 3} Założenia zrobiłem na końcu, ponieważ łatwiej je odczytać, jak wszystkie wyrażenia są rozłożone na czynniki.

Gustlik: ad 2a)

	−4		−4		−12
f(x)=		+7=		+7=		+7=
	1   x−   3		3x−1   3		3x−1

	−12+7(3x−1)		−12+21x−7
=		=		=
	3x−1		3x−1

	21x−19
=
	3x−1

Gustlik: ad 2 b)

	1,5x−9
f(x)=
	x+2

Dzielę licznik przez mianownik jak wielomiany i wyciągam "całości" − ta sama zasada, co wyciąganie całości z ułamków "liczbowych", wynik dzielenia to całości, a reszta to licznik ułamka: 1,5 −−−−−−−−−−−−−−−−−−−− (1,5x−9):(x+2) −1,5x−3 −−−−−−−−−− = −12

	−12
f(x)=		+1,5
	x+2

Gustlik: ad 3 a)

4x−16
	=0
4−3x

Dziedzina: 4−3x≠0 −3x≠−4 /:(−3)

	4
x≠
	3

	4
D=R\{		}
	3

Ułamek = 0 ⇔ licznik = 0 4x−16=0 4x=16 /:4 x=4 ∊D (sprawdzam z dziedziną !)

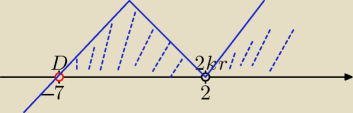
Gustlik: ad 3 b)

x2−5x−3
	>−1
x+7

Dziedzina: x+7≠0 x≠−7 D=R\{−7}

x2−5x−3
	+1>0
x+7

x2−5x−3+x+7
	>0 ("wciągam" 1 na wspólny mianownik i wymnażam z mianownikiem stąd to x+7
x+7

w liczniku)

x2−4x+4
	>0
x+7

Zamieniam na iloczyn (znak będzie ten sam): (x²−4x+4)(x+7)>0 (x−2)²(x+7)>0 i rozwiazuję jak nierówność wielomianową x=2 (2−krotny − wykres "odbije" się od osi X) lub x=−7 (dziedzina − puste kółko !) x∊(−7, 2)U(2, +∞)

asdf: @Gustlik Witam, czemu mnoży się * (x + 7)², a nie sam mianownik się liczy ?

Gustlik: Nie rozumiem, skąd wziąłeś mnozenie *(x+7)² ?

asdf:

x2 − 4x + 4
	> 0 || *(x + 7)2
x + 7

(x² − 4x + 4)(x + 7) > 0

Gustlik: Dzieleniem i mnożeniem "rządzą" takie same reguły znakowe, czyli:

a
	>0 ⇔ a*b>0
b

a
	≥0 ⇔ a*b≥0
b

a
	<0 ⇔ a*b<0
b

a
	≤0 ⇔ a*b≤0
b

Krótko mówiąc: ułamek ma zawsze ten sam znak, co iloczyn licznika i mianownika, stąd zamiana ułamka na iloczyn.

	x2−4x+4
Wyrażenie		ma więc taki sam znak jak (x2−4x+4)(x+7).
	x+7

Nierówności wymiernej nie można mnożyć przez sam mianownik, czyli przez x+7, bo nie wiemy, jaki jest znak wyrażenia x+7 i w zwiazku z tym nie wiemy, czy ">" zamieni się na "<" czy nie. Trzeba byłoby robić założenia, a z tym byłaby podobna zabawa, jak z nierównościami z wartością bezwzględną − kupę rozpisywania i załozeń. Dlatego prosciej jest zamienić ułamek na iloczyn lub − jak słusznie zauważyłeś − pomnożyć przez wyrażenie (x+7)², które wiemy, że przy założeniu x≠−7 jest dodatnie, więc znak ">" się nie zmieni.

asdf: Dzięki za wyjaśnienie Przy równaniach jest ta sama zasada? (chcę być pewien) P.S "Nierówności wymiernej nie można mnożyć przez sam mianownik, czyli przez x+7, bo nie wiemy, jaki jest znak wyrażenia x+7 i w zwiazku z tym nie wiemy" x + 7 tu nie powinno być x² − 4x + 4?

Gustlik: Przy równaniach można mnożyc przez mianowniki, bo "=" to "=", niezależnie od znaku mianownika, natomiast mnożenie i dzielenie nierówności przez liczbę ujemną odwraca znak nierówności w drugą stronę, np. z ">" na "<". Np.

x
	=6 /*(−2)
−2

x=−12 ale !

x
	>6 /*(−2)
−2

x<−12 Jeżeli w mianowniku jest liczba, to wiemy, czy znak się odwróci, czy nie, a jeżeli jest wielomian, np. x+7, x²−3x−4 itd., to znak ">" zachowa się w zależności od znaku tego wielomianu i gdybyś chciał mnożyć, musiałbyś rozpatrywać co najmniej 2 przypadki wraz z założeniami − jak pisałem − byłaby zabawa, jak przy wartosciach bezwzględnych − kupę pisaniny i łatwo się pomylić. Dlatego w nierówności wymiernej postępujemy zawsze tak, żeby prawa stronę wyzerować, a w lewej "zdobić" jeden ułamek, czyli: 1. Ustalamy dziedzinę wyrażeń wymiernych. 2. Przenosimy wszystkie wyrażenia (ułamki, wielomiany, liczby itp.) z prawej strony na lewą, po prawej stronie musi zostać 0. 3. Sprowadzamy lewą stronę do wspólnego mianownika. 4. Zamieniamy ułamek stojący po lewej stronie na iloczyn licznika i mianownika, rozkładamy ewentualnie wielomiany na czynniki (o ile się da) i otrzymana nierówność rozwiązujemy jak nierówność wielomianową, pamiętając o dziedzinie (czyli "puste" kropki na wykresie przy pierwiastkach mianownika, nawet przy znakach "≥", "≤" − ja je oznaczam literą "D" − dziedzina)

asdf: Raz jeszcze, dziękuje bardzo

Gustlik: Pozdrawiam

bst: mama pytanie do ad3 b. jakbym było > −2 to po przeniesiuniu byłoby +2 ale wtedy tzreba by było pomnożyć mianownik i byłoby 2x+14? tak? ad2 b − nie rozumiem ; (1,5x−9):(x+2) −1,5x−3 −−−−−−−−−− = −12

bst:

	4x−16
mam jeszcze 1 zadanie Dana jest funkcja f(x) =
	3x−4

a.podaj dziedzine tej funkcji. b.oblicz miejsca zerowe c.zapisz rownania asymptot wykresu tej funkcji.

	1
d.oblicz dla jakiego argumentu funkcja przyjmuje wartosc 1
	4

	1
dziedzina x różne od 1
	3

a reszta?

Gustlik: ad 3 b) TAK. ad 2b) Zapoznaj się z dzieleniem wielomianów − naprawdę WARTO ! Jest ono podobne do dzielenia pisemnego liczb. Krótko mówiąc: dzielisz pierwszy wyraz pierwszego wielomianu przez pierwszy wyraz drugiego wielomianu, a wynik wpisujesz na górze. Ten wynik potem mnożysz przez drugi nawias i wpisujesz ze zmienionym znakiem (tak jak w dzieleniu liczb wynik dzielenia mnożysz przez dzielnik − drugą liczbę i odejmujesz). Do wyniku odejmowania dopisujesz następny składnik wielomianu, tak jak w dzieleniu liczb dopisujesz kolejna cyfrę itd. do końca. Dzielenie wielomianów: https://matematykaszkolna.pl/strona/107.html .

	4x−16
f(x)=
	3x−4

	a
Przekształcam wzór z postaci ogólnej do kanonicznej y=		+q metodą dzielenia wielomianów.
	x−p

4
3

−−−−−−−−−−−−−−−−−−−−−− (4x−16):(3x−4)

	1
−4x+5
	3

−−−−−−−−−−−−−−−−−−

	2
−10
	3

	2   −10   3		4		32   −   3		4
f(x)=		+		=		+		=
	3x−4		3		3x−4		3

	−32		4		−32		4
=		+		==		+		=
	9x−12		3		12   9(x− )   9		3

	32   −   9		4
=		+
	4   x−   3		3

	4		4
p=		, q=
	3		3

	4
ad b) Dziedzina D=R\{p}=R\{		}
	3

Miejsca zerowe − tu lepiej skorzystać ze wzoru ogólnego niż z kanonicznego:

4x−16
	= 0
3x−4

4x−16=0 4x=16 /:4 x=4

	4		4
ad c) Asymptoty: x=p, y=q, czyli x=		, y=
	3		3

ad d)

4x−16		5
	=		i mnożysz na krzyż
3x−4		4

4(4x−16)=5(3x−4) 16x−64=15x−20 16x−15x=64−20 x=44

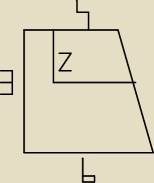
bst: jeszcze prosze o pomoc z tym to "Z" tj 2 1.Wewnątrz trapezu prostokątnego ABCD zbudowano trapez do niego podobny Oblicz pole szarej figury. Pole calego trapezu wyszło mi 15j² ale nie wiem jak znalesc "dół" tego mniejszego żeby odjąc bo nie jest to 4.

asdf: proporcje ułóż

bst: asdf jak?

bst: JEZIORO MA POWIERZCHNIĘ 200HA. OBLICZ JAKA JEST POW. TEGO JEZIORA NA MAPIE W SKLAI 1;20000 m=20000 D=200ha=200*200*200*200cm i co z tym zrobić ? pomocy na jutro muszę to umieć wszystko

bst:

3		2
	=		tak? to wychodzi 4 ...
6		X

bst: P¹=15 P⁼ 4x

	15
x=		= 3.75
	4

tak to ma być?

Gustlik: Pole dużego trapezu:

	6+4		10
P1=		*3=		*3=15
	2		2

Skala podobieństwa − dzielę odpowiadające sobie boki:

	2
k=
	3

Pole małego trapezu:

	4		4		20		2
P2=k2*P1=		*15=		*5=		=6
	9		3		3		3

Pole pozostałej figury:

	2		1
P=P1−P2=15−6		=8
	3		3

Gustlik: 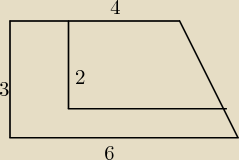bst liczby i litery zamiast rysować możesz normalnie wpisywać − klikasz ikonę z literą "T" (tekst) w narzędziach rysowania po prawej stronie rysunku, potem klikasz w miejsce na rysunku, gdzie chcesz wstawić literę lub liczbę i wpisujesz tę literę z klawiatury, a w przypadku innych znaków, np. α, β, γ z ikonek nad polem tekstu. Bedzie to wyglądało czytelniej − tak jak na powyższym rysunku. Bo na Twoim rysunku "2" wygląda jak "z" i zacząłem się zastanawiać, jak Ci pomóc − za dużo wychodziło niewiadomych, dopiero z Twojego późniejszego postu skapowałem sie, że "z" to "2".

Gustlik: JEZIORO MA POWIERZCHNIĘ 200HA. OBLICZ JAKA JEST POW. TEGO JEZIORA NA MAPIE W SKLAI 1;20000 Przeliczam ha na cm², bo w tych jednostkach będzie wygodniej ją liczyć na mapie i potem powierzchnię jeziora też na cm²: 1 ha = 100 a = 10000 m² = 10000 * 10000 cm²= 100 000 000 cm² P₁ = 200 ha = 200 * 100 000 000 cm² = 20 000 000 000 cm² − powierzchnnia jeziora "w realu"

	1
P2 = k2*P1=(		)2 * 20 000 000 000 cm2 =
	20000

	1
=		* 20 000 000 000 cm2 = 50 cm2
	400 000 000

Odp: P₂=50 cm²

pigor: ... Jezioro ma powierzchnię 200ha. Oblicz jego powierzchnię na mapie w skali 1:20000. otóż, z danej skali mapy wynika, że 1cm na mapie = 20000cm = 200*100cm = 200m = 2*100m w terenie, to 1cm² na mapie = 4*(100m)² = 4*100m*100m = 4 ha w terenie zatem w terenie 200 ha = 4 ha * 50 = 1 cm² * 50 = 50 cm² na mapie . ...

bst: DZIĘKÓWA ŻYCZCIE MI POWODZENIA NA 9 EGZAMIN

bst: ZDANE DZIEKOWA WSZYSTKIM